1 感知器模型

1.1 起源

感知器模型与算法由美国科学家 Frank Rosenblatt 于 1958 年提出，最早用于解决图像分类问题。我们把向量 $ \begin{equation} x = (x_1, x_2, … , x_n)^T \end{equation} $ 称为模式（Pattern）或特征（Feature）向量，比如 $ \begin{equation} x_i \end{equation} $ 表示图像中第 i 个像素的亮度。标量 y 称为类别标号（Class label）。感知器可以把一个模式 x 区分为两个不同的类别 $ \begin{equation} (y = -1, +1) \end{equation} $ ，这个过程称为分类（Classification）。

1.2 定义

假设输入空间（特征空间）是 $ \begin{equation} \mathcal{X} \in R^n \end{equation} $ ，输出空间是 $ \begin{equation} \mathcal{Y} \in \lbrace -1, 1 \rbrace \end{equation} $ ，其中输入 $ \begin{equation} x \in \mathcal{X} \end{equation} $ 表示实例的特征向量，对应于输入空间（特征空间）的点，输出 $ \begin{equation} y \in \mathcal{Y} \end{equation} $ 表示实例的类别，有输入空间到输出空间的函数：

\begin{equation} g(x; w, b) = sgn(w^Tx + b) \end{equation}

称为感知器。其中 g 称为决策函数，sgn 称为符号函数：

\begin{equation} sgn(x) = \begin{cases} \ \ \ 1, &x \geqslant 0\\ -1, &x < 0 \end{cases} \end{equation}

由判别函数得到一个方程：

\begin{equation} \mathcal{f} (x; w, b) = w^Tx + b = 0 \end{equation}

该方程是一个线性方程，表示 d 维空间的一个超平面（hyper-plane），称为决策面（Decision Boundary），把该空间划分两半，位于该决策面一侧的样本 x 为正样本（y = 1）、位于另一侧的样本为负样本（y = -1），w 为该超平面的法向量，b 为位置偏置。图 1 展示了 d = 2 时的情况。

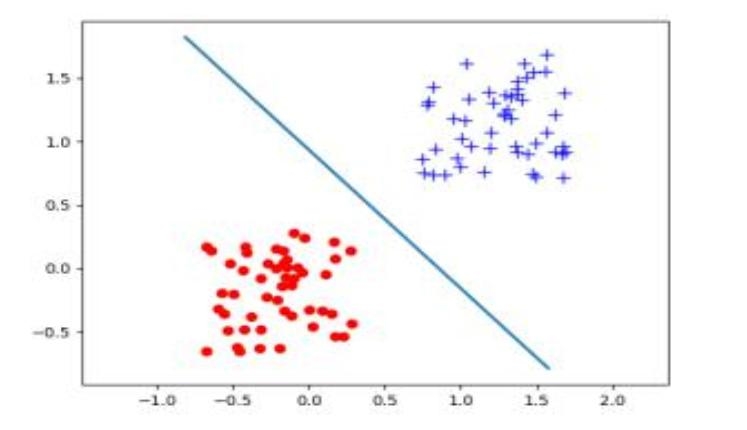
图1 线性决策面

由于 d 维感知器的决策面是一个超平面，因此一个感知器只能对可以用超平面分隔的样本进行区分，如果样本的分布不能用线性超平面区分（线性不可分），那么单个感知器就无法起作用。比如图 2 中的红色与蓝色样本，是线性不可分的。

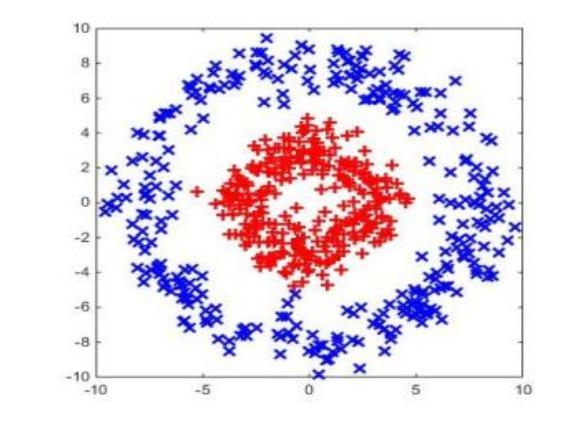
图2 线性不可分

2 感知器学习算法

2.1 定义

感知器模型由参数 $ \begin{equation} \Theta = (w, b ) \end{equation} $ 决定。但是在很多问题中，这些参数无法由人工决定。比如，图像分类中，权值 $ \begin{equation} w_i \end{equation} $ 表示第i个像素的权值，这个权值很难由人工分析确定。因此需要有一种方法能自动确定这些参数。在机器学习中，如果给定一组已知类别标号的样本集 $ \begin{equation} D = \lbrace (x^{(i)}, y^{(i)}) \rbrace (i = 1, 2, …, n) \end{equation} $ ，那么可以从这组样本中学习（Learning）/训练（Training）出模型的参数 $ \begin{equation} \Theta \end{equation} $ 。
感知器学习算法（Perceptron Learning Algorithm，PLA）是 Rosenblatt 给出的一个用于学习感知器模型的算法。该算法是一个迭代算法，首先初化模型参数为 w = 0，b = 0，假设第 t 步得到的模型参数为 $ \begin{equation} \Theta = (w, b ) \end{equation} $ ，在 t + 1 步，从 D 中选取一个样本 $ \begin{equation} (x^{(j)}, y^{(j)}) \end{equation} $ ，用当前模型参数代入感知器中对该样本进行分类，得到分类结果为 $ \begin{equation} \bar y \end{equation} $ 。如果分类正确（ $ \begin{equation} \bar y = y^{(j)} \end{equation} $ ），那么权值不变；如果分类错误（ $ \begin{equation} \bar y \neq y^{(j)} \end{equation} $ ），根据类别标号 $ \begin{equation} y = y^{(j)} \end{equation} $ 对权值做如下更新：

\begin{equation}\begin{split} &w \leftarrow w + y^{(j)}x^{(j)} \\ &b \leftarrow b + y^{(j)} \end{split}\end{equation}

2.2 PLA算法（伪代码）

下面的伪代码展示了感知器的学习过程：

当训练样本集D是线性可分时，上述算法在有限步内能输出一个能对D中所有样本正确分类的模型$ \begin{equation} g(x; w, b) \end{equation} $。

2.3 PLA算法实现

  1. 算法思想：对样本集进行重复迭代，以实现逐点修正。
    • ① 获取样本集中本次迭代的样本的预测值 $ \begin{equation} \bar y \end{equation} $ 。
    • ② 将预测值 $ \begin{equation} \bar y \end{equation} $ 和该样本的真实值 $ \begin{equation} y^{(i)} \end{equation} $ 进行比较。
      • 分类正确，对样本集中的下一个样本进行预测，即跳转到 ① 处执行，直至样本集中的样本全部迭代，然后跳转至③。
      • 分类错误，标记出现错误分类，然后对 $ \begin{equation} \vec w \end{equation} $ 和 b 进行更新，完成后跳转到 ① 处执行，直至样本集中的样本全部迭代，然后跳转至③。
    • ③ 若样本集中的所有样本全部迭代，且未出现错误分类，即说明当前的权重和偏差值正确，输出此时的 $ \begin{equation} \vec w \end{equation} $ 和 b 。
  2. Java实现：
  • PLA算法核心
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 重复迭代样本集实现逐点修正
while (true){
    boolean flag = true;    // 错误分类标记（用于判断当前w、b是否可以实现二分类）
    Collections.shuffle(data);  // 对测试集进行随机排序
    for (Data d : data) {   // 迭代样本集
        int y_hat = forecast(weight, b, d); // 预测值
        int y = d.getY();   // 真实值
        if (y * y_hat <= 0){  // 判断当前分类是否正确，>0正确
            flag = false;   // 出现错误分类
            weight = update(weight, d); // 更新权重
            b += d.getY();  // 更新偏差值
        }
    }
    if (flag)	// 本次迭代未出现错误分类
        break;
}
  • forecast(Weight weight, int b, Data data)方法
1
2
3
4
5
6
7
8
9
10
11
/**
 * 计算y_hat(预测值)
 * @param weight    权重
 * @param b         偏差值
 * @param data      数据集
 * @return          返回预测值
 */
public static int forecast(Weight weight, int b, Data data){
    return ((weight.getW1() * data.getX1()) + (weight.getW2() * data.getX2()) + b);
}

  • update(Weight weight, Data data)方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * 更新权重
 * @param weight    原权重值
 * @param data      数据集
 * @return          返回更新后的权重
 */
public static Weight update(Weight weight, Data data){
    // 获取样本数据
    int x1 = data.getX1();
    int x2 = data.getX2();

    // 获取实际值
    int y = data.getY();

    // 更新权重
    int newW1 = weight.getW1() + (y * x1);
    int newW2 = weight.getW2() + (y * x2);
    weight.setW1(newW1);
    weight.setW2(newW2);
    return weight;
}
  • 运行结果

（1）运行结果1

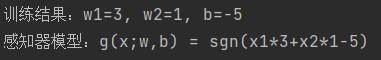
（2）运行结果2

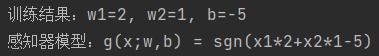
（3）运行结果3

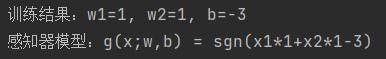
（4）运行结果4

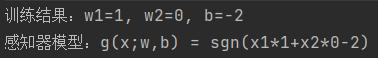
3 总结

  • 感知器主要可以解决线性可分的问题，他可以用来解决二分类问题，其具有如下的优点和缺点：
    • 优点：相较于其他模型，感知器模型简单，易于实现。
    • 缺点：
      • PLA算法每一次运行的结果不一致（不稳定），所以无法完美的处理线性不可分的训练集（数据）。
      • 感知机中的损失函数（衡量预测值与真实值之间的误差）的目标只是减小所有误分类点与超平面，最终很有可能导致部分样本点距离超平面很近。所以通过PLA得到的只是一个近似最优解的解，并不能得到最优解。
  • 导致PLA算法第一个缺点的主要原因是因为该算法的基本原理是逐点修正。首先，在超平面上随意取一条分类面，统计分类错误的点，然后随机对某个错误点进行修正，也就是改变直线的位置，使该错误点得以修正；接着再随机选一个错误点进行纠正，分类面不断变化，直到所有的点都完全分类正确了，就得到了最佳的分类面。正是因为每次运行PLA算法进行的是一种随机修正，所以得到的结果不一样。
  • PLA算法的第二个确定可以通过SVM（支持向量机）解决，另外SVM也可以很好地解决线性不可分问题。