1. 背景介绍
1.1 1 vs 1
最基本的单层网络:单个输入单个输出
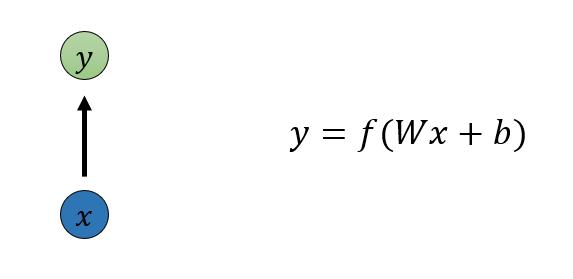
1.2 N vs N: RNN
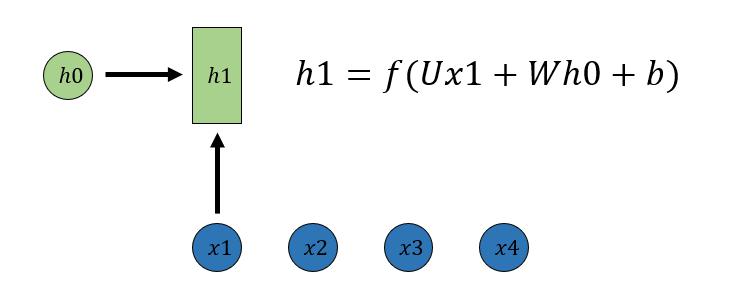
序列形的数据不太好用原始神经网络处理。为了建模序列问题,RNN引入了隐状态h(hidden state)的概念,h可以对序列形的数据提取特征,接着再转换为输出。h1的计算如下所示:
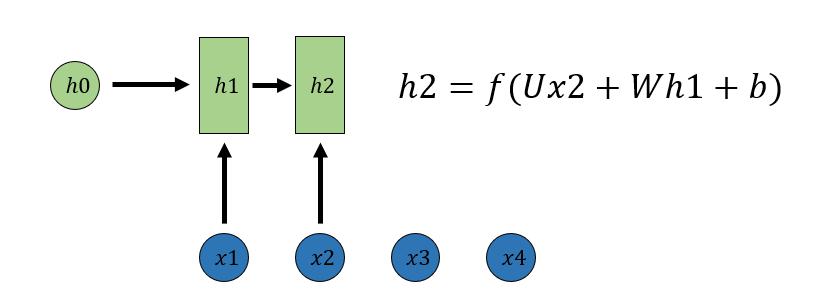
h2的计算和h1类似。值得注意的是,在计算时,每一步使用的参数U、W、b都是一样的,即每个步骤的参数都是共享的。
依次计算剩下来的(使用相同的参数U、W、b):
ℎ3=𝑓(𝑈𝑥3+𝑊ℎ2+𝑏)
ℎ4=𝑓(𝑈𝑥4+𝑊ℎ3+𝑏)
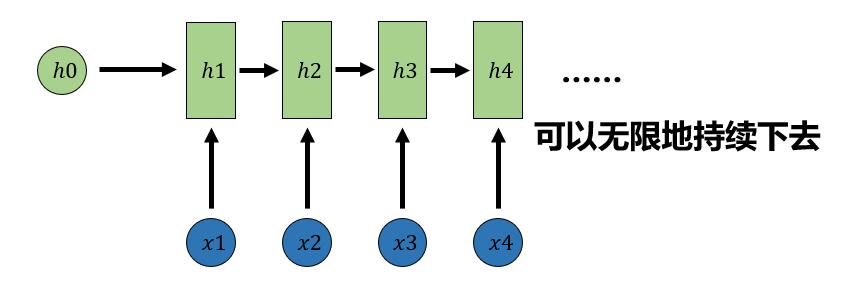
直接通过h进行计算得到RNN的输出:
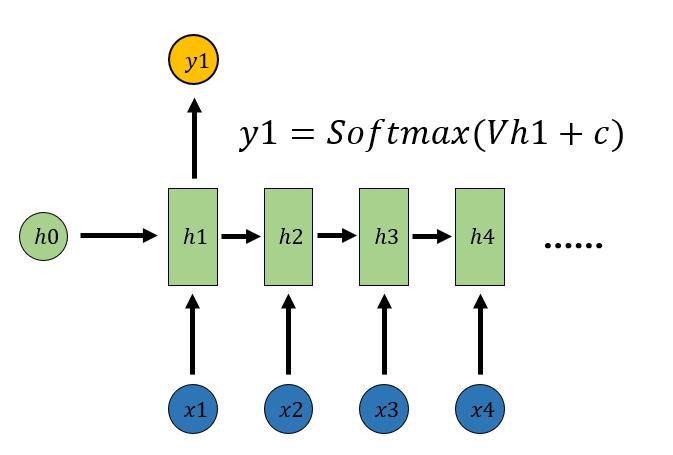
剩下的输出类似进行(使用和y1同样的参数)
𝑦2=𝑆𝑜𝑓𝑡𝑚𝑎𝑥(𝑉ℎ2+𝑐)
𝑦3=𝑆𝑜𝑓𝑡𝑚𝑎𝑥(𝑉ℎ3+𝑐)
𝑦4=𝑆𝑜𝑓𝑡𝑚𝑎𝑥(𝑉ℎ4+𝑐)
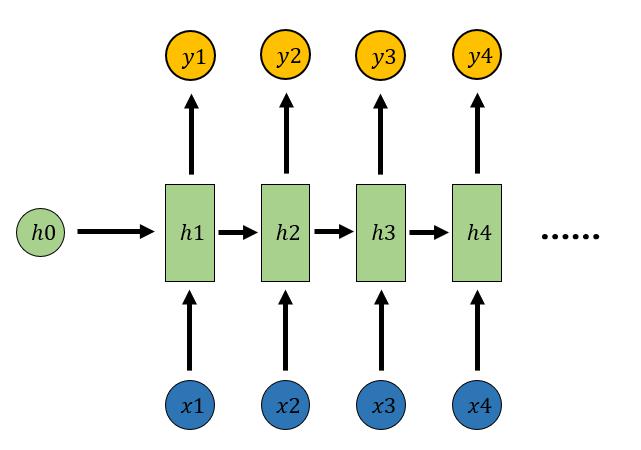
- 计算视频中每一帧的分类标签
- 输入为字符,输出为下一个字符的概率
- ……
1.3 N vs 1
输入是一个序列,输出一个值,通常用来处理序列分类问题
𝑦=𝑆𝑜𝑓𝑡𝑚𝑎𝑥(𝑉ℎ4+𝑐)
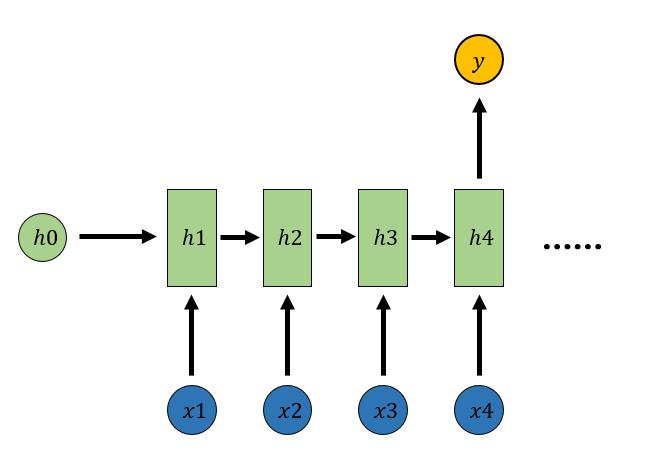
- 输入一段文字判别它所属的类别
- 输入一个句子判断其情感倾向
- 输入一段视频并判断它的类别
- ……
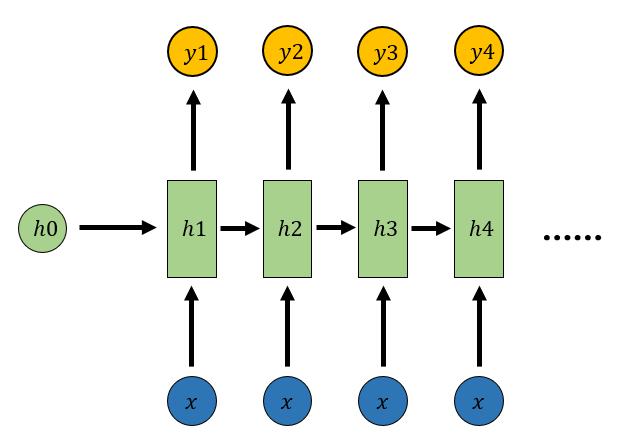
1.4 1 vs N
输入是一个值,输出是一个序列
𝑦1=𝑆𝑜𝑓𝑡𝑚𝑎𝑥(𝑉ℎ1+𝑐)
𝑦2=𝑆𝑜𝑓𝑡𝑚𝑎𝑥(𝑉ℎ2+𝑐)
𝑦3=𝑆𝑜𝑓𝑡𝑚𝑎𝑥(𝑉ℎ3+𝑐)
𝑦4=𝑆𝑜𝑓𝑡𝑚𝑎𝑥(𝑉ℎ4+𝑐)
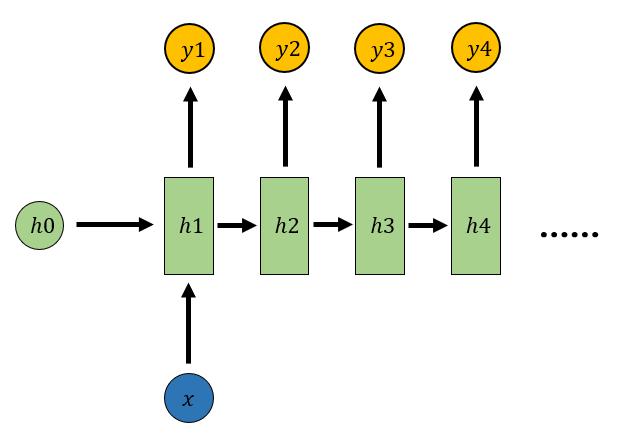
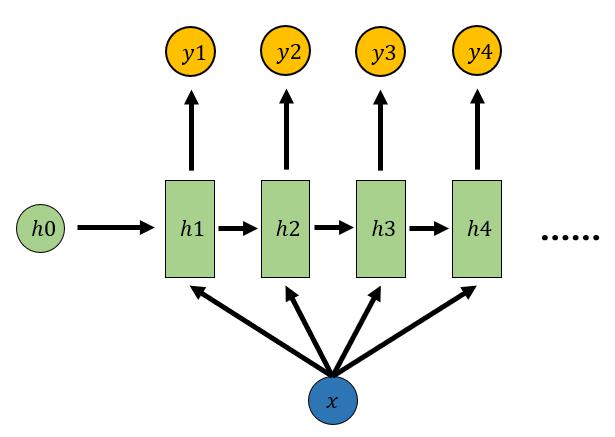
- 从图像生成文字
- 从类别生成语音或音乐等
- ……
1.5 N vs M: Sequence-to-sequence(Seq2seq)
输入一个序列,输出一个序列,输出序列的长度由模型决定
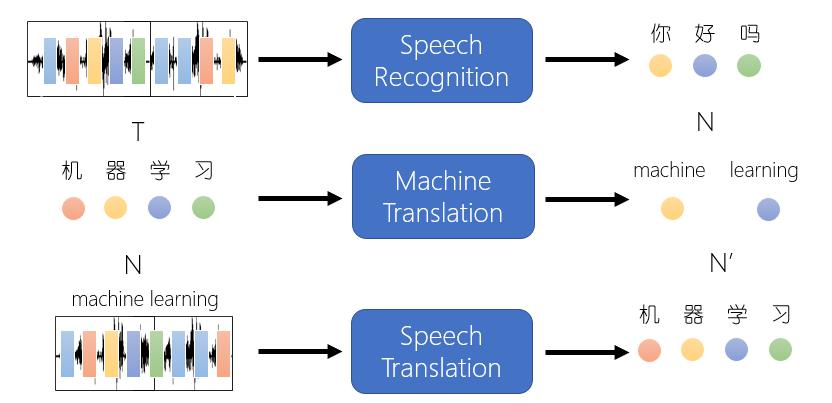
输入一个序列,输出一个序列,这种结构又叫Encoder-Decoder模型,也可以称之为Seq2Seq模型
Encoder-Decoder结构先将输入数据编码(Encoder)成一个上下文向量c:
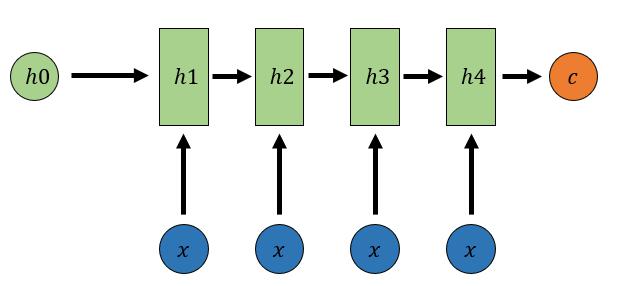
(1) 𝑐=ℎ4
(2) 𝑐=𝑞(ℎ4)
(3) 𝑐=𝑞(ℎ1,ℎ2,ℎ3,ℎ4)
用另一个RNN网络对其进行解码(Decoder):
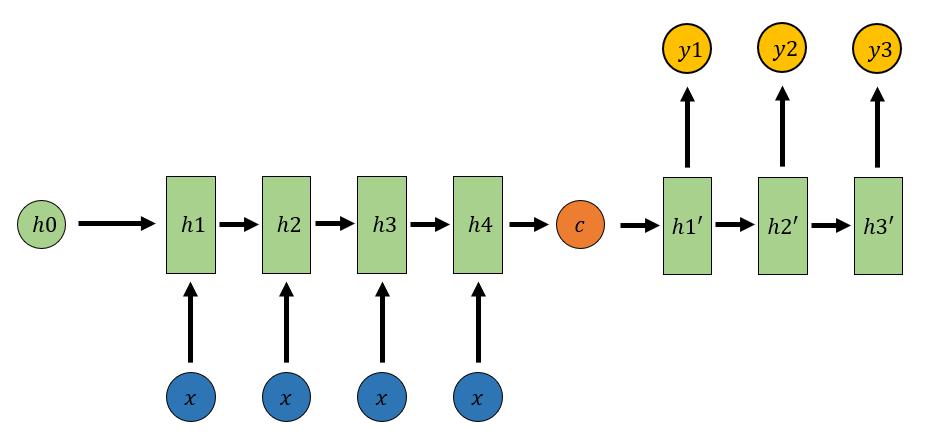
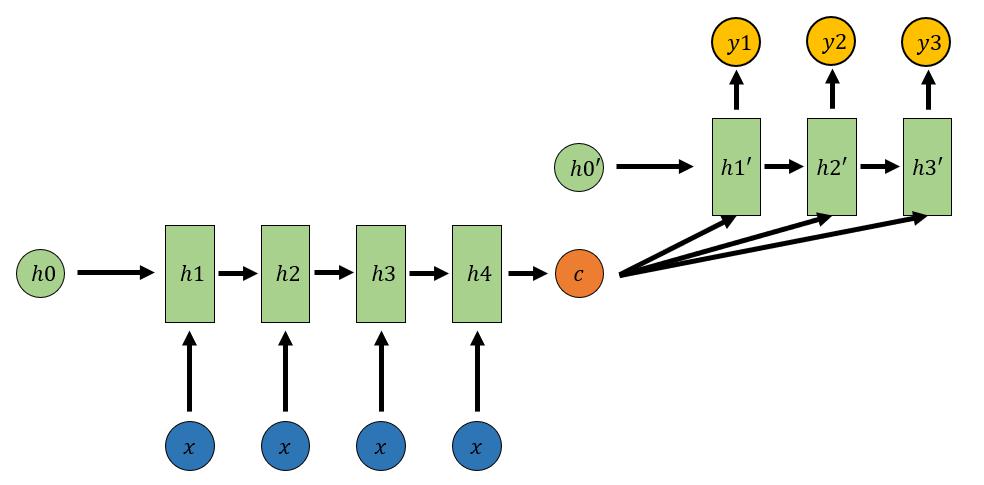
Encoder-Decoder结构不限制输入和输出的序列长度,因此应用的范围非常广泛:
- 机器翻译:Encoder-Decoder最先就是在机器翻译领域最先提出的
- 文本摘要:输入一段文本序列,输出这段文本序列的摘要序列
- 阅读理解:将输入的文章和问题分别编码,再对其进行解码得到问题的答案
- 语音识别:输入是语音信号序列,输出是文字序列
- ……
1.6 Seq2seq
在Seq2Seq结构中,编码器Encoder把所有的输入序列都编码成一个统一的语义向量Context,然后再由解码器Decoder解码。在解码器Decoder解码的过程中,不断地将前一个时刻t-1的输出作为后一个时刻t的输入,循环解码,直到输出停止符为止。
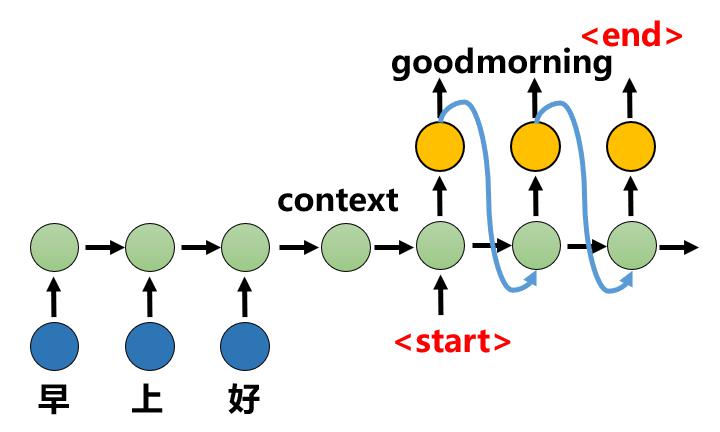
Seq2seq训练问题
在seq2seq结构中将 𝑦_𝑡作为下一时刻输入𝑥_(𝑡+1) 进网络,那么某一时刻输出 错误就会导致后面全错。在训练时由于网络尚未收敛,这种蝴蝶效应格外明显
Scheduled Sampling:在训练中𝑥_𝑡按照一定概率选择输入 𝑦_(𝑡−1)或 t-1时刻对应的真实值,即标签,既能加快训练速度,也能提高训练精度。
基于Attention的Seq2seq
通俗理解Attention:SE模块最终是学习出一个1x1xc的向量,然后逐通道乘以原始输入,从而对特征图的每个通道进行加权即通道注意力
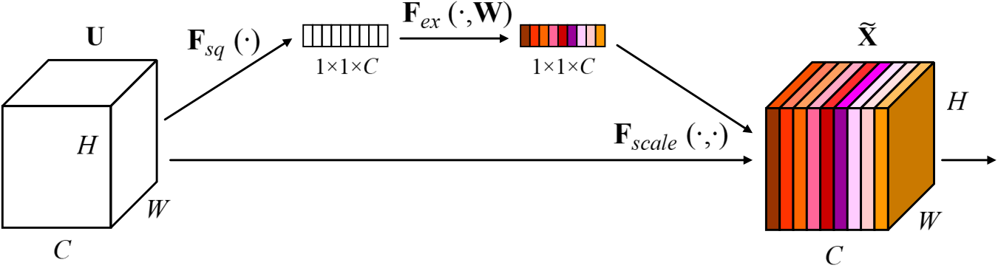
Attention机制通过在每个时间输入不同的c来解决c长度受限问题,带有Attention机制的Decoder如下图所示:
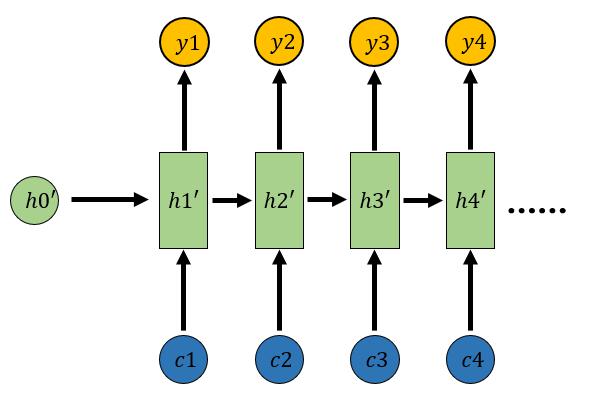
- 每一个c会自动去选取与当前所要输出的y最合适的上下文信息。
- 用$ \begin{equation} a_{ij} \end{equation} $衡量Encoder中第j阶段的hj和解码时第i阶段的相关性,最终Decoder中第i阶段的输入的上下文信息 ci就来自于hj对 $ \begin{equation} a_{ij} \end{equation} $的加权和
如何得到权重$ \begin{equation} 𝒂_{𝒊𝒋} \end{equation} $?
从模型中学习,和Decoder的第i-1阶段的隐状态、Encoder第j个阶段的隐状态有关
基于attention的seq2seq的结构的缺陷:
- 不管是采用RNN、LSTM还是GRU都不利于并行训练和推理,因为相关算法只能从左向右依次计算或者从右向左依次计算。无法并行训练,不利于大规模快速训练和部署,也不利于整个算法领域发展。
- 长依赖信息丢失问题,顺序计算过程中信息会丢失,虽然LSTM号称有缓解,但是无法彻底解决
2. Transformer
2.1 简介
Transformer结合self-attention和cross-attention进行了改进。
在encode阶段,重点学习输入元素之间的attention。在decode阶段,重点学习的输出查询与encode的结果之间的attention。
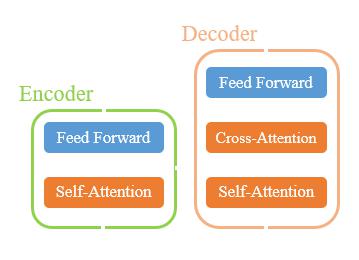
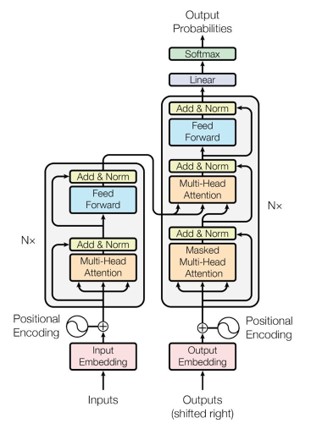
深入分析
- Q和所有K计算相似性
- 对相似性采用softmax转化为概率分布
- 将概率分布和V进行一一对应相乘,最后相加得到新的和Q一样长的向量输出
编码器输入数据处理
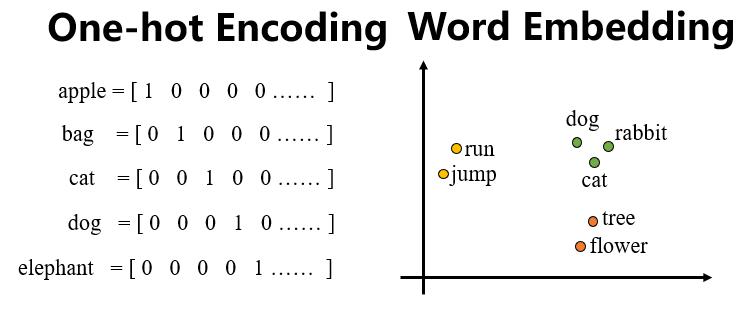
- 方法一:开一个很长的One-hot Encoding向量,忽略了词汇与词汇之间的关系
- 方法二:Word embedding,含有语义信息
Embedding:任何一个单词,都可以被映射成为唯一的一个N维向量
2.2 Positional encoding
Transformer内部没有类似RNN的循环结构,没有捕捉顺序序列的能力,或者说无论句子结构怎么打乱,transformer都会得到类似的结果。为了解决这个问题,在编码词向量时会额外引入了位置编码position encoding向量表示两个单词i和j之间的距离,简单来说就是在词向量中加入了单词的位置信息
- 网络自动学习
- 自己定义规则
网络自动学习
网络自动学习

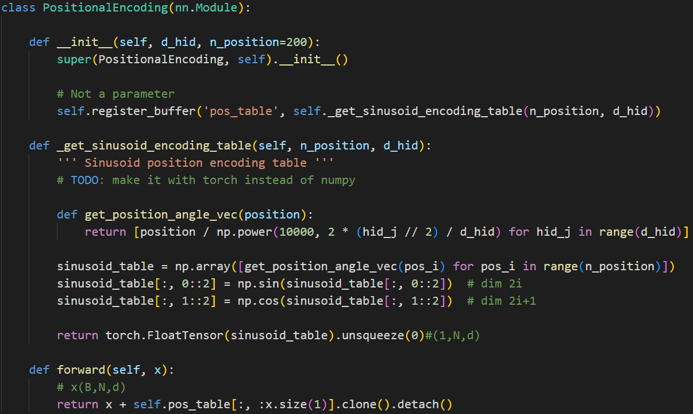
比较简单,因为位置编码向量需要和输入embedding(b,N,512)相加,所以其shape为(1,N,512)表示N个位置,每个位置采用512长度向量进行编码
自己定义规则:sin-cos规则
- 将向量的512维度切分为奇数行和偶数行
- 偶数行采用sin函数编码,奇数行采用cos函数编码
- 然后按照原始行号拼接
2.3 Self-Attention
编码器前向过程
对于自注意力层self-attention来讲,Q(Query), K(Key), V(Value)三个矩阵均来自同一输入
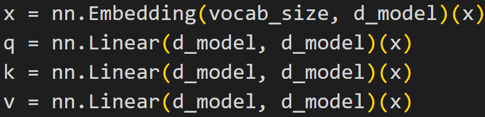
1) 从每个编码器的输入向量创建三个向量。分别是查询向量Q、键向量K、值向量V
2) 通过查询向量与正在评分的各个单词的关键向量的点积来计算分数
Self-Attention的矩阵计算
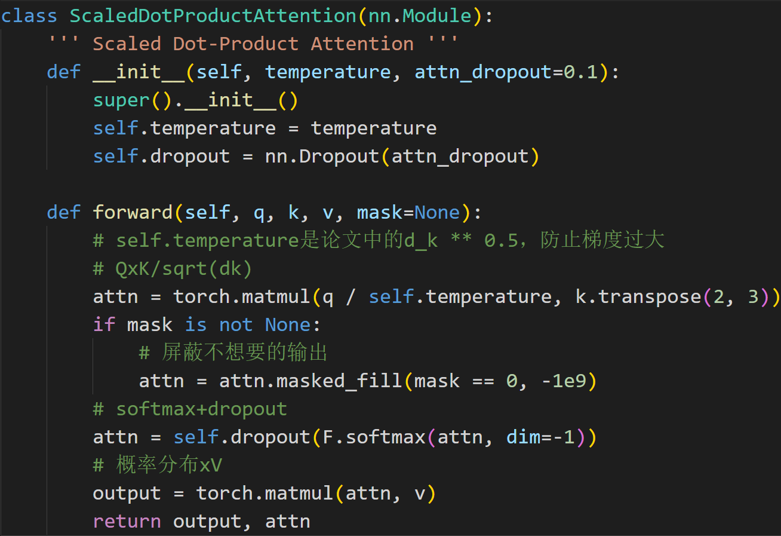
1) 计算查询、键和值矩阵。通过将Embedding打包到矩阵X中,并将其乘以训练的权重矩阵(WQ、WK、WV)
2)计算自注意力层的输出
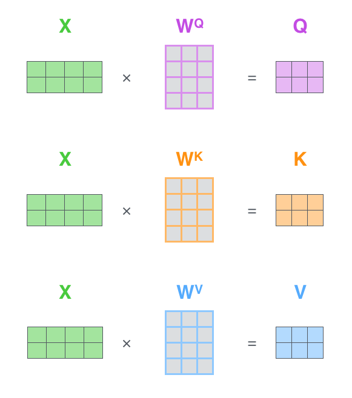
Self-Attention的代码实现
先令 $ \begin{equation} 𝑸∗𝑲^𝑻 \end{equation} $ ,再对结果按位乘以 Mask矩阵,再做 Softmax操作,最后的结果与 V相乘,得到self-attention的输出
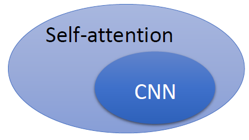
self-attention vs CNN
- self-attention在处理一张图片的时候,1的那个pixel产生query,其他的各个pixel产生key。在做inner-product的时候,考虑的不是一个小的范围,而是一整张图片。
- CNN只考虑感受野红框里面的资讯,而不是图片的全局信息。所以CNN可以看作是一种简化版本的self-attention。
- self-attention是一种复杂化的CNN,在做CNN的时候是只考虑感受野红框里面的信息,而感受野的范围和大小是由人决定的。但是self-attention由attention找到相关的pixel,就好像是感受野的范围和大小是自动被学出来的,所以CNN可以看做是self-attention的特例。
- self-attention是更广义的CNN,则这个模型更加flexible。一个模型越flexible,训练它所需要的数据量就越多,所以在训练self-attention模型时就需要更多的数据,这一点在下面介绍的论文 ViT 中有印证,它需要的数据集是有3亿张图片的JFT-300,而如果不使用这么多数据而只使用ImageNet,则性能不如CNN。
2.4 Multi-head Self-Attention
- 它扩展了模型关注不同位置的能力
- 为注意力层提供了多个“表示子空间”
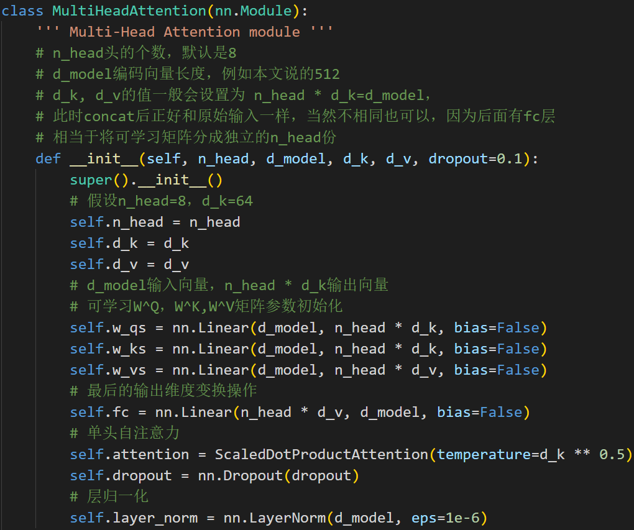
Multi-head Self-Attention的代码实现
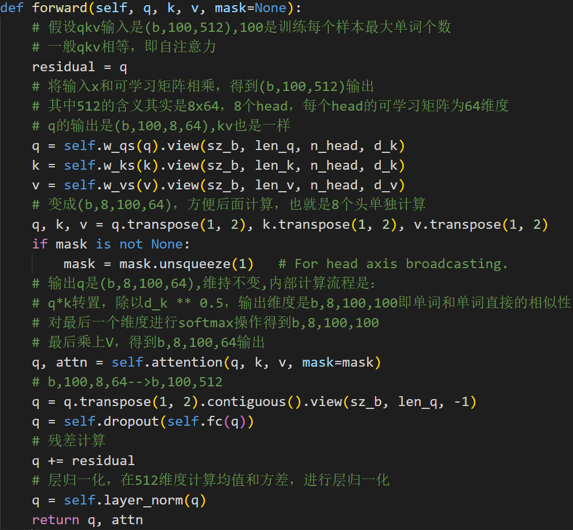
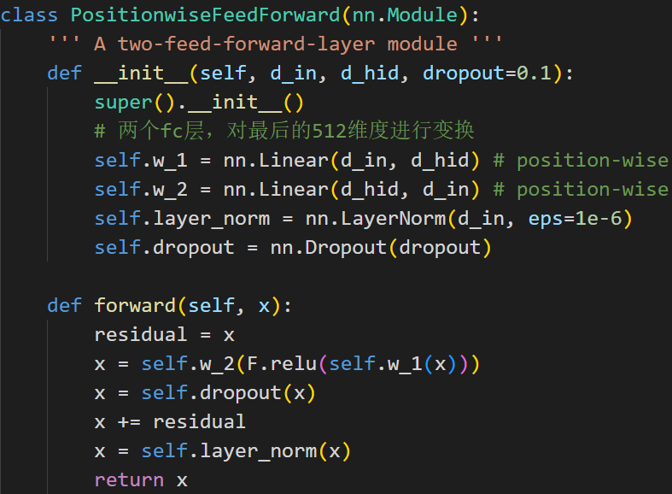
前馈神经网络层的代码实现
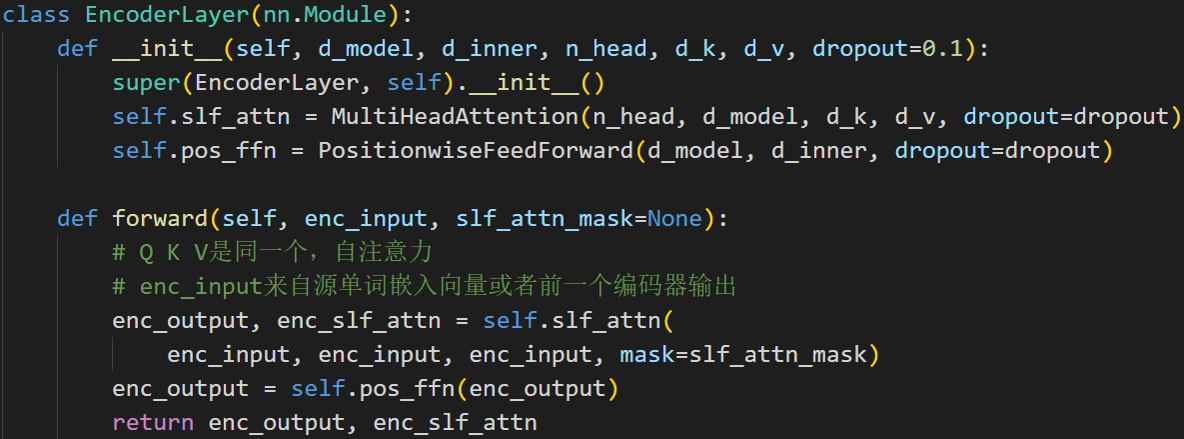
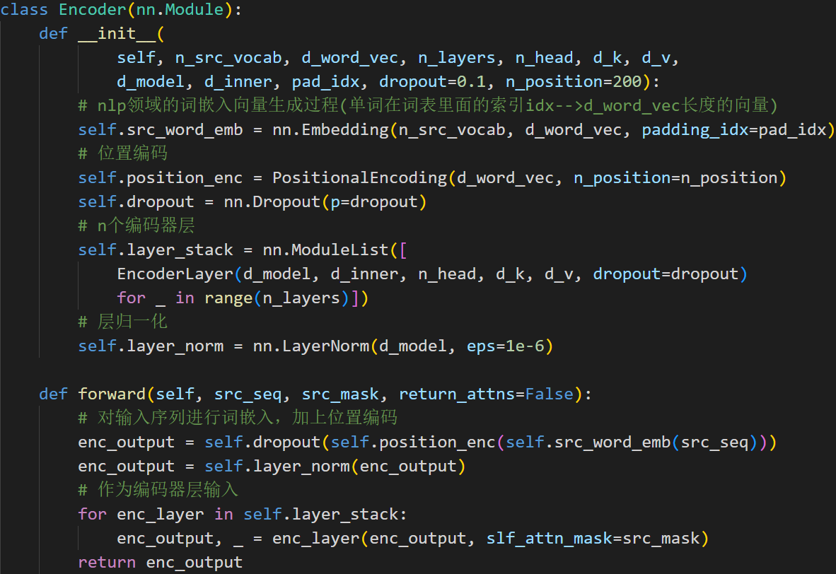
单个编码层的代码实现
除了第一个模块输入是单词嵌入向量与位置编码的和外,其余编码层输入是上一个编码器输出即后面的编码器输入不需要位置编码向量
2.5 Masked Multi-Head Self-attention
为什么需要mask?
训练时:不采用上述类似RNN的方法一个一个目标单词嵌入向量顺序输入训练,想采用类似编码器中的矩阵并行算法,一步就把所有目标单词预测出来。要实现这个功能就可以参考编码器的操作,把目标单词嵌入向量组成矩阵一次输入即可。即:并行化训练。
但是在解码have时候,不能利用到后面单词a和cat的目标单词嵌入向量信息,否则这就是作弊(测试时候不可能能未卜先知)。为此引入mask。具体是:在解码器中,self-attention层只被允许处理输出序列中更靠前的那些位置,在softmax步骤前,它会把后面的位置给隐去(把它们设为-inf) 。为此引入mask,目的是构成下三角矩阵,右上角全部设置为负无穷(相当于忽略),从而实现当解码第一个字的时候,第一个字只能与第一个字计算相关性,当解出第二个字的时候,只能计算出第二个字与第一个字和第二个字的相关性。
解码器内部的带有mask的MultiHeadAttention的qkv向量输入来自目标单词嵌入或者前一个解码器输出,三者是相同的,但是后面的MultiHeadAttention的qkv向量中的kv来自最后一层编码器的输入,而q来自带有mask的MultiHeadAttention模块的输出
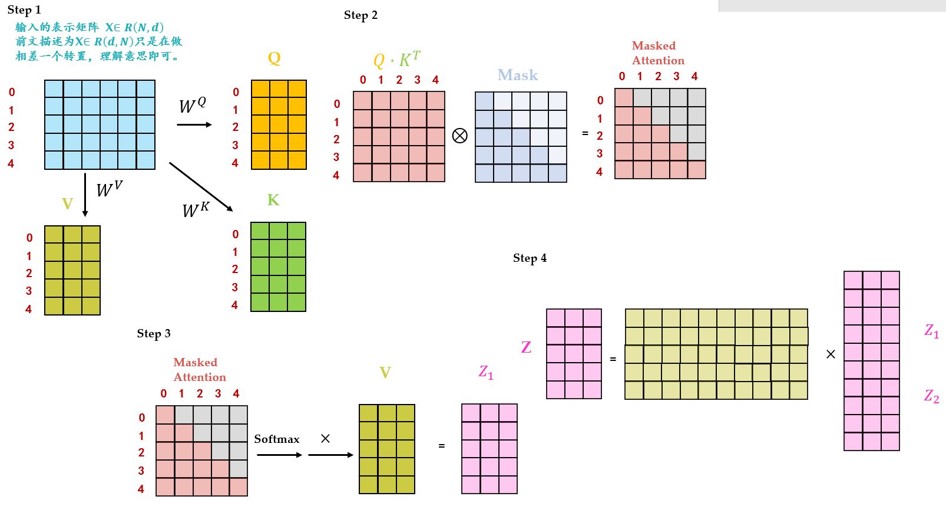
Masked Multi-Head Self-attention的具体操作:
- Step1:输入矩阵包含 “<Begin> I have a cat” (0, 1, 2, 3, 4) 五个单词的表示向量,Mask是一个 5×5 的矩阵。在Mask可以发现单词 0 只能使用单词 0 的信息,而单词 1 可以使用单词 0, 1 的信息,即只能使用之前的信息。
- Step2: 𝑸^𝑻∗𝑲得到 Attention矩阵,此时先不急于做softmax的操作,而是先于一个Mask矩阵相乘,使得attention矩阵的有些位置归0,得到Masked Attention矩阵。 Mask矩阵是个下三角矩阵,为什么这样设计?是因为想在计算Z矩阵的某一行时,只考虑它前面token的作用。即:在计算Z的第一行时,刻意地把Attention矩阵第一行的后面几个元素屏蔽掉。在产生have这个单词时,只考虑 I,不考虑之后的have a cat,即只会attend on已经产生的sequence,这个很合理,因为还没有产生出来的东西不存在,就无法做attention。
- Step3:Masked Attention矩阵进行 Softmax,每一行的和都为 1。但是单词 0 在单词 1, 2, 3, 4 上的 attention score 都为 0。得到的结果再与V矩阵相乘得到最终的self-attention层的输出结果Z1。
- Step4: Z1只是某一个head的结果,将多个head的结果concat在一起之后再最后进行Linear Transformation得到最终的Masked Multi-Head Self-attention的输出结果Z。
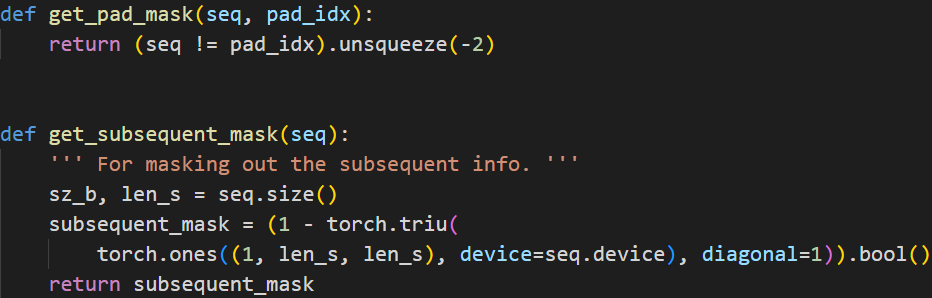
Mask的代码实现
src_mask = get_pad_mask(src_seq, self.src_pad_idx)
用于产生Encoder的Mask,它是一列Bool值,负责把标点mask掉。
trg_mask = get_pad_mask(trg_seq, self.trg_pad_idx) & get_subsequent_mask(trg_seq)
用于产生Decoder的Mask矩阵。
单个解码层的代码实现
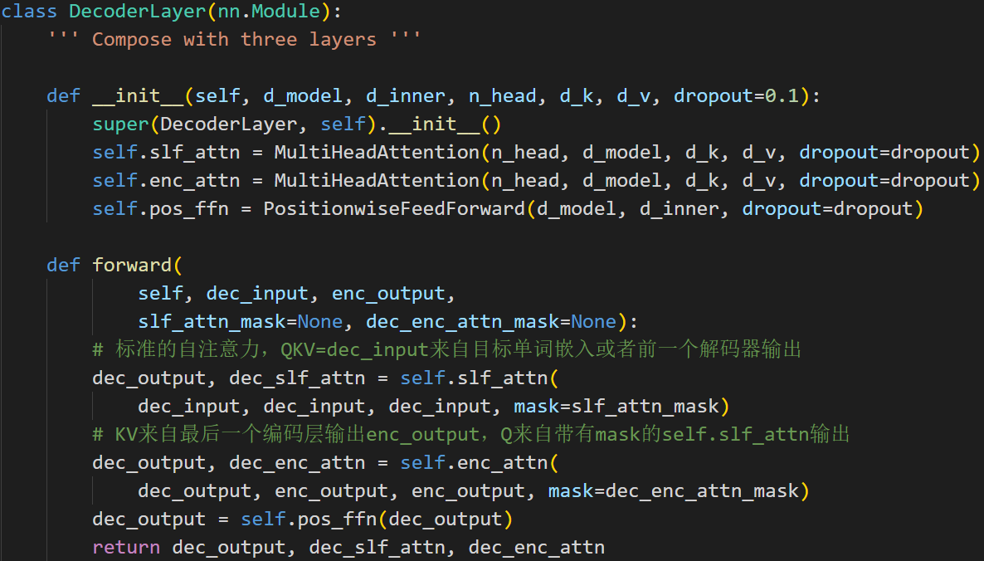
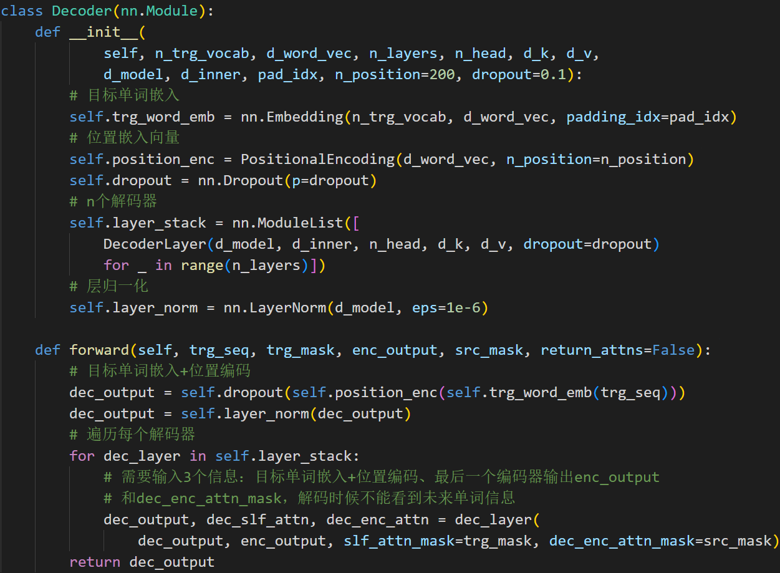
多个解码层的代码实现
2.6 传统Attention、Self Attention、Cross Attention
- 传统的Attention是基于source端和target端的隐变量计算Attention的,得到的结果是source端的每个词与target端每个词之间的依赖关系。
- 传统的Attention是基于source端和target端的隐变量计算Attention的,得到的结果是source端的每个词与target端每个词之间的依赖关系。
- Self -Attention分别在source端和target端进行自身的attention,仅与source input或者target input自身相关的Self -Attention,以捕捉source端或target端自身的词与词之间的依赖关系。
- Cross-Attention把source端的得到的self -Attention加入到target端得到的Attention中,以捕捉source端和target端词与词之间的依赖关系。
- 传统的Attention机制忽略了源端或目标端句子中词与词之间的依赖关系,self Attention可以不仅可以得到源端与目标端词与词之间的依赖关系,同时还可以有效获取源端或目标端自身词与词之间的依赖关系。
3. 视觉领域的Transformer
3.1 Transformer+Classification:Vision Transformer
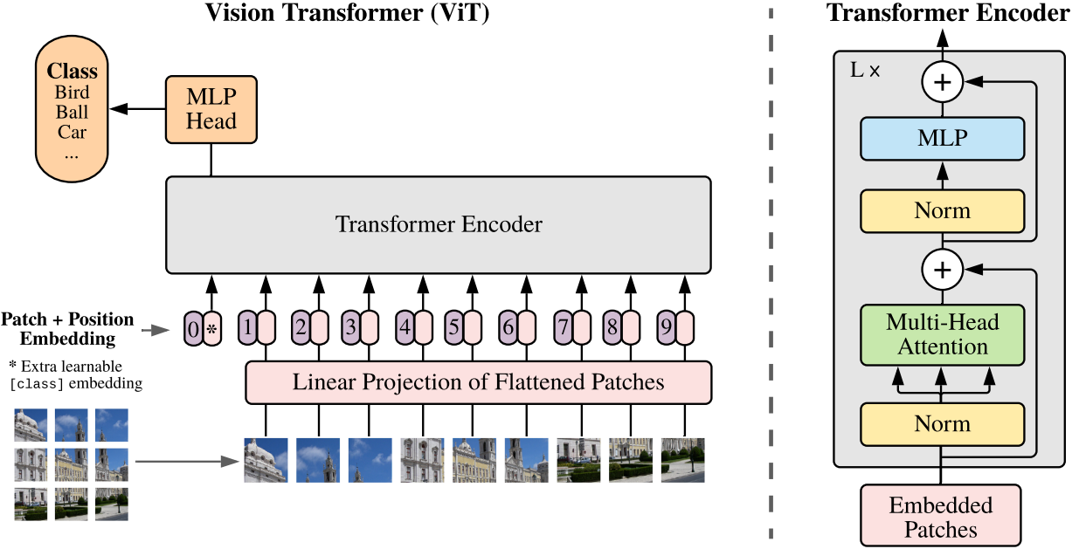
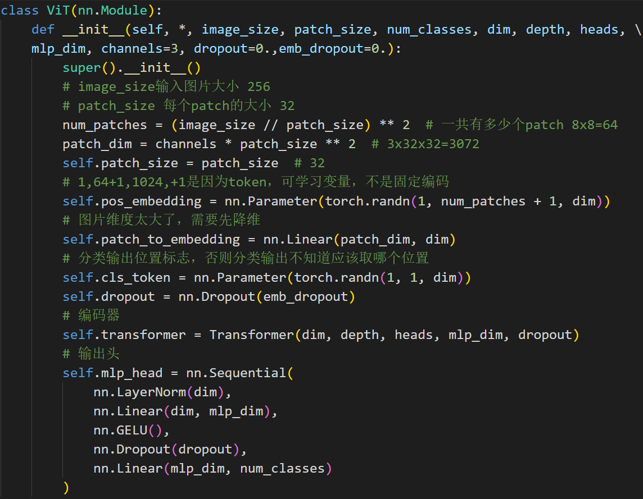
图片分块和降维
transformer的输入需要序列,最简单做法就是把图片切分为patch,然后拉成序列即可。 假设输入图片大小是256x256,打算分成64个patch,每个patch是32x32像素:

P代表patch大小,假设输入是b,3,256,256,则rearrange操作是先变成(b,3,8x32,8x32),最后变成(b,8x8,32x32x3)即(b,64,3072),将每张图片切分成64个小块,每个小块长度是32x32x3=3072,也就是说输入长度为64的图像序列,每个元素采用3072长度进行编码。
考虑到3072维度偏大,故先对其进行降维:

没有解码器如何执行分类预测?
使用CLS Token整合输出信息
Class的作用有点类似于解码器中的Query的作用,相对应的Key,Value就是其他9个编码向量的输出
在整合图片信息时,一种是使用CLS Token,另一种是对所有Tokens的输出取平均,两者可以达到同样效果: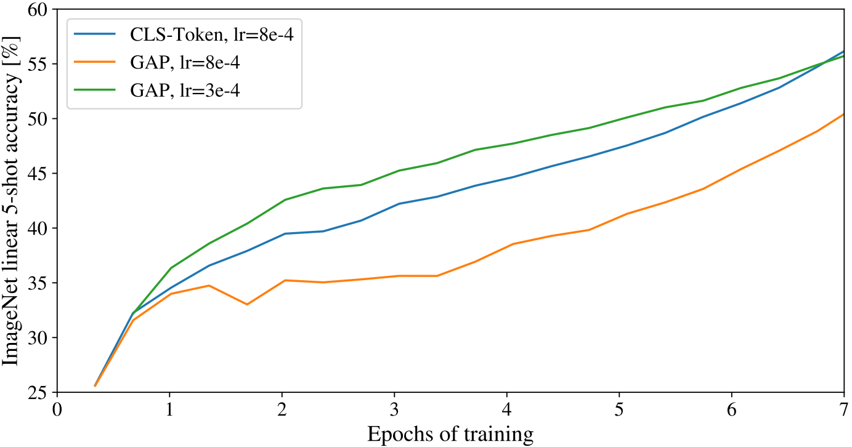
位置编码
位置编码长度为1024,本文没有采用sincos编码,而是直接设置为可学习。
位置越接近,往往具有更相似的位置编码。此外,出现了行列结构;同一行/列中的patch具有相似的位置编码。

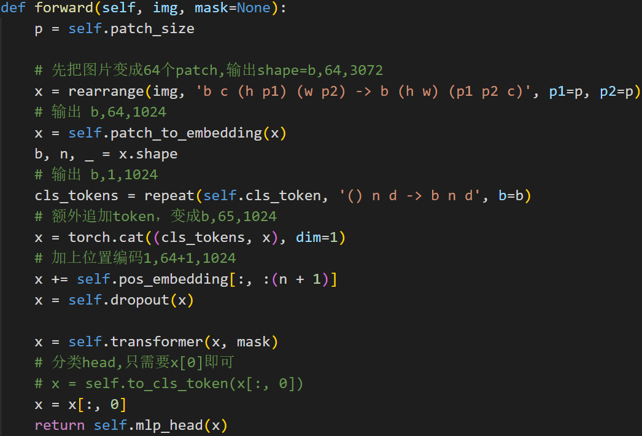
编码器前向过程
没有任何改动的transformer,假设输入是(b,65,1024),那么transformer输出也是(b,65,1024)

分类head
编码器后接fc分类器head
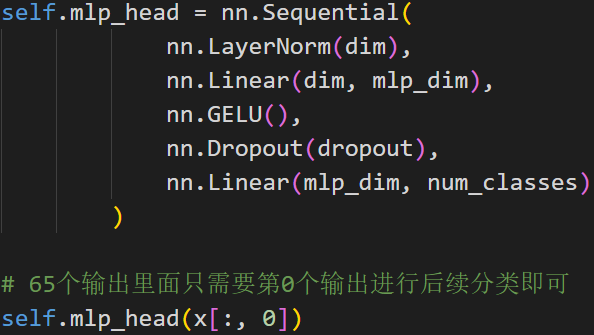
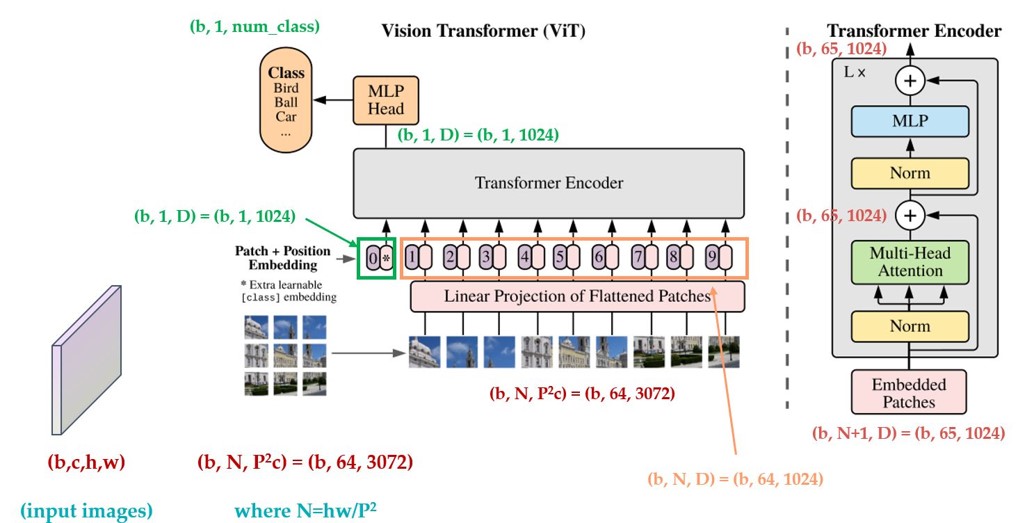
VIT整体流程:
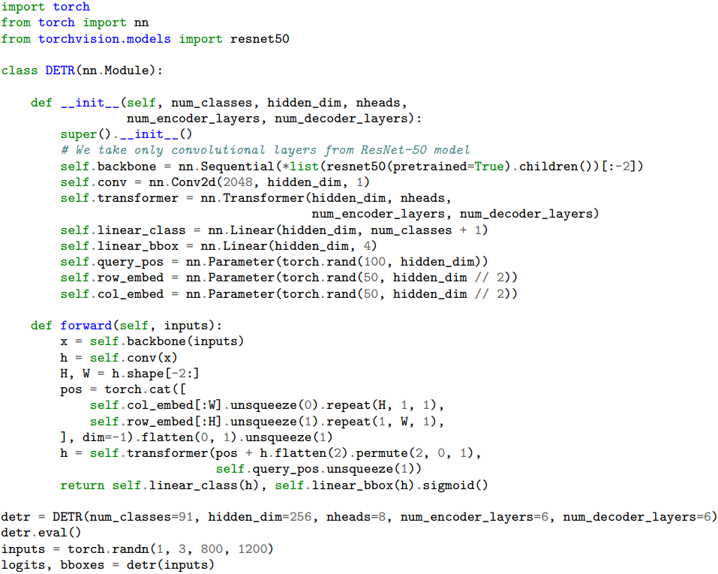
3.2 Transformer+Detection:DETR
- 用transformer的encoder-decoder架构一次性生成 N个box prediction。其中N是一个事先设定的、比远远大于image中object个数的一个整数。将目标检测问题转化为无序集合预测问题。
- 设计了bipartite matching loss,基于预测的boxes和ground truth boxes的二分图匹配计算loss的大小,从而使得预测的box的位置和类别更接近于ground truth。
- 不需要设置先验anchor和proposal;超参很少;不需要nms(end to end)
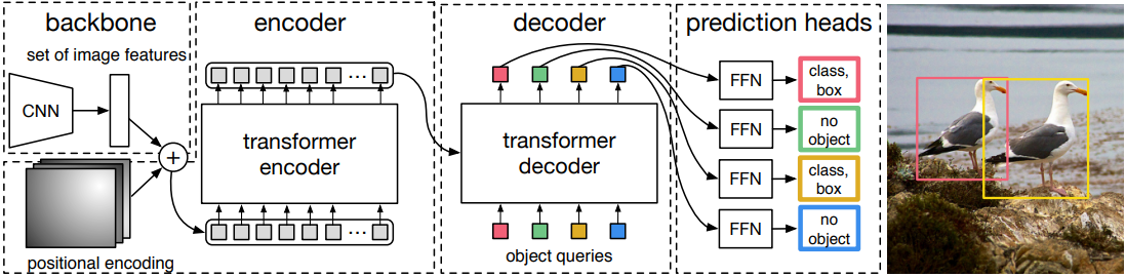
cnn主干网络特征提取
主干网络可以是任何一种,作者选择resnet50,将最后一个stage即stride=32的特征图作为编码器输入。由于resnet仅仅作为一个小部分且已经经过了imagenet预训练,故和常规操作一样,会进行如下操作:
- resnet中所有BN都固定,即采用全局均值和方差
- resnet的stem和第一个stage不进行参数更新,即parameter.requires_grad_(False)
- backbone的学习率小于transformer,lr_backbone=1e-05,其余为0.0001
假设输入是(b,c,h,w),则resnet50输出是(b,2048,h//32,w//32),2048比较大,为了节省计算量,先采用1x1卷积降维为256,最后转化为序列格式输入到transformer中,输入shape=(h’xw’,b,256),h’=h//32

编码器设计和输入
位置编码需要考虑2d空间
DETR考虑了xy方向的位置编码,因为图像特征是2-D特征。采用的依然是 sincos模式,但是需要考虑 xy两个方向。不是类似vit做法将其拉伸为一个向量,然后从0-n进行长度为256的位置编码,而是考虑了xy方向同时编码,每个方向各编码128维向量,这种编码方式更符合图像特点。
Positional Encoding的输出张量是:(B,d,H,W),其中 d代表位置编码的长度, H,W代表张量的位置。特征图上的任意一个点(H1,W1)有个位置编码,这个编码的长度是256,其中,前128维代表 H1的位置编码,后128维代表H2的位置编码。
计算任意一个位置 ($ \begin{equation} 𝒑𝒐𝒔_𝒙 \end{equation} $, $ \begin{equation} 𝒑𝒐𝒔_𝒚 \end{equation} $) 的Positional Encoding,把 $ \begin{equation} 𝒑𝒐𝒔_𝒙 \end{equation} $代入右式的 a式和 b式可以计算得到128维的向量,它代表 x的位置编码,再把 $ \begin{equation} 𝒑𝒐𝒔_𝒚 \end{equation} $ 代入右式的 c式和 d式可以计算得到128维的向量,它代表 y的位置编码,把这2个128维的向量拼接起来,就得到了一个256维的向量,它代表 ($ \begin{equation} 𝒑𝒐𝒔_𝒙 \end{equation} $, $ \begin{equation} 𝒑𝒐𝒔_𝒚 \end{equation} $) 的位置编码。
计算所有位置的编码,就得到了(256,H,W)的张量,代表这个batch的位置编码。编码矩阵的维度是 (B,256,H,W),也把它序列化成维度为 (HW,B,256)维的张量,准备与(HW,B,256)维的feature map相加以后输入Encoder。
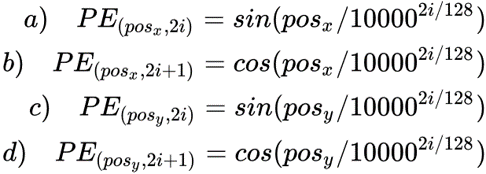
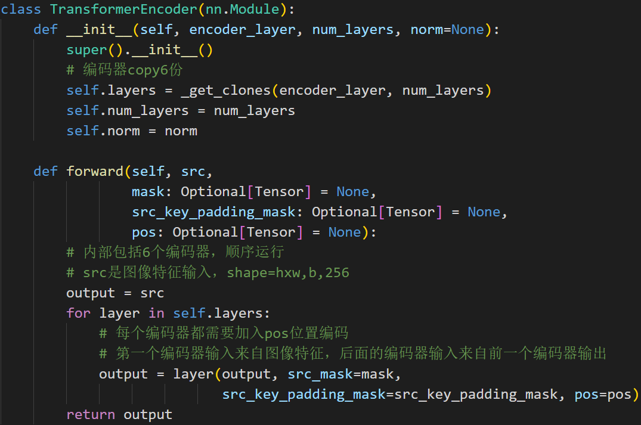
与原始transformer编码器不同的地方:
- 输入编码器的位置编码需要考虑2d空间位置
- 位置编码向量需要加入到每个编码器中
- 在编码器内部位置编码仅仅和QK相加,V不做任何处理
代码实现:
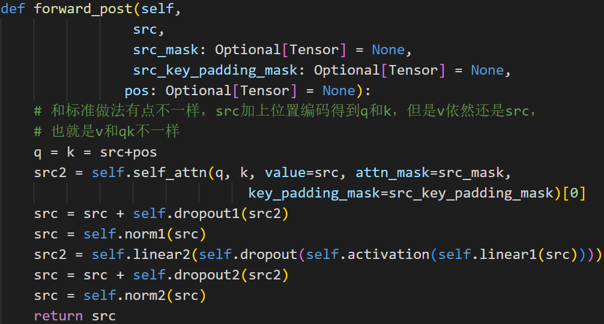
解码器设计和输入
- Transformer Encoder输出的Embedding与 position encoding 之和。
- Object queries。
Object queries是一个维度为(100,b,256)维的可学习张量,充当位置编码作用。
Object queries矩阵内部通过学习建模了100个物体之间的全局关系,例如房间里面的桌子旁边(A类)一般是放椅子(B类),而不会是放一头大象(C类),那么在推理时候就可以利用该全局注意力更好的进行解码预测输出。
Decoder的输入一开始也初始化成维度为 (100,b,256)维的全部元素都为0的张量,和Object queries加在一起之后充当第1个multi-head self-attention的Query和Key。第一个multi-head self-attention的Value为Decoder的输入,也就是全0的张量。
对Encoder和Decoder的每个self-attention的Query和Key的位置编码的归纳
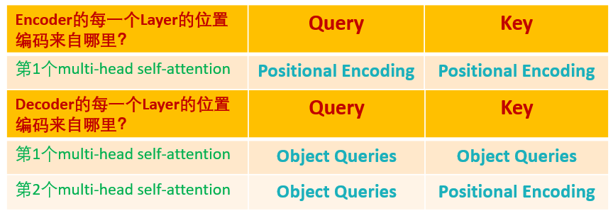
无序集合输出的loss计算:
DETR输出是包括(b,100)个无序集合,每个集合包括类别c[长度为92的分类向量]和坐标信息(x,y,w,h)[长度为4的坐标向量],故DETR输出集合包括两个分支:
- 分支shape=(b,100,92),bbox坐标分支shape=(b,100,4)
- 对应的target也是包括分类target和bbox坐标target,如果不够100,则采用背景填充,计算loss时候bbox分支仅仅计算有物体位置,背景集合忽略。
匈牙利算法: 广泛应用于最优分配的二分图匹配问题
的bx100个检测结果是无序的,如何和gt bbox计算loss?
DETR中利用匈牙利算法先进行最优一对一匹配得到匹配索引,然后对(b,100)个结果进行重排实现和gt bbox对应。优化的目的是找到最优匹配排列,使得L_match和最小。
代码实现:
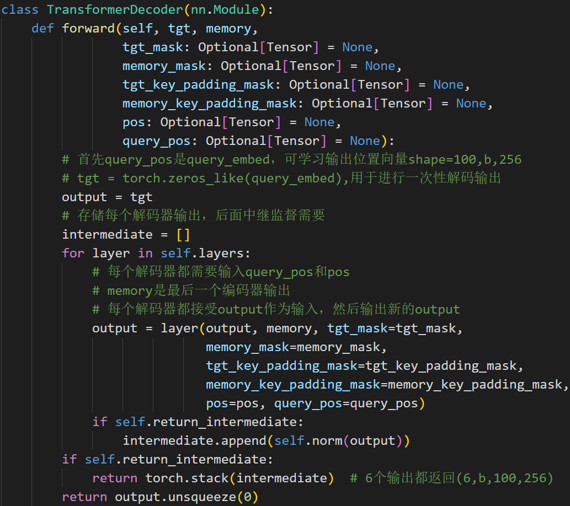
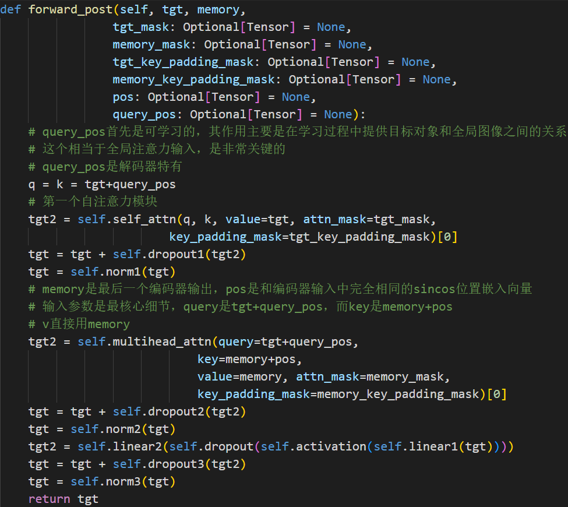
分类和回归head
在解码器输出基础上构建分类和bbox回归head即可输出检测结果
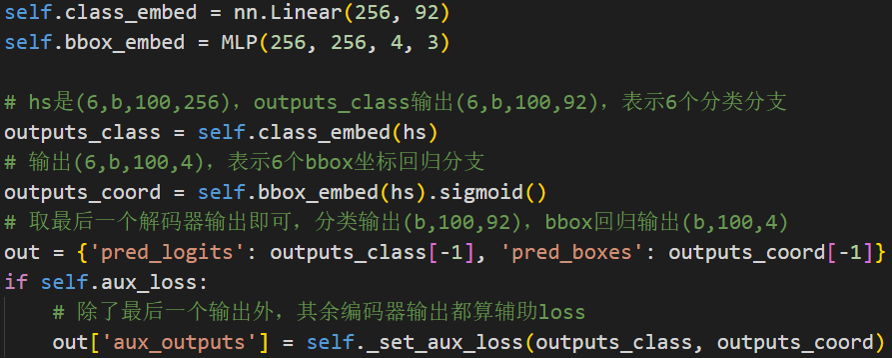
- 模型学习到了什么?
训练完以后,DETR模型学习到了一种能力,即:模型产生的100个预测框,它知道某个预测框该对应什么Object,比如,模型学习到:第1个预测框对应 Car(label=3),第2个预测框对应 Bus(label=16) ,第3个预测框对应 Sky(label=21) ,第4-100个预测框对应 ∅(label=92),等等- Object queries学习到了什么?
它是一个维度为(100,b,256)维的张量,初始时元素全为 0,是可训练的。考虑单张图片,所以假设Object queries是一个维度为 (100,256)维的张量。训练完模型以后,此时的Object queries究竟代表什么?
把Object queries看成100个格子,每个格子是个256维的向量。训练完以后,这100个格子里面注入了不同Object的位置信息和类别信息。比如第1个格子里面的这个256维的向量代表着Car这种Object的位置信息,这种信息是通过训练,考虑了所有图片的某个位置附近的Car编码特征,属于和位置有关的全局Car统计信息。测试时,假设图片中有Car,Dog,Hourse三种物体,该图片会输入到编码器中进行特征编码,假设特征没有丢失,Decoder的Key和Value就是编码器输出的编码向量,而Query就是Object queries,就是我们的100个格子。
Query可以视作代表不同Object的信息,而Key和Value可以视作代表图像的全局信息。
通过注意力模块将Query和Key计算,然后加权Value得到解码器输出。对于第1个格子的Query会和Key中的所有向量进行计算,目的是查找某个位置附近有没有Car,如果有那么该特征就会加权输出,对于第3个格子的Query会和Key中的所有向量进行计算,目的是查找某个位置附近有没有Sky,很遗憾,这个没有,所以输出的信息里面没有Sky。
整个过程计算完成后就可以把编码向量中的Car,Dog,Hourse的编码嵌入信息提取出来,然后后面接 FFN进行分类和回归就比较容易,因为特征已经对齐了。
整体推理流程
- 将(b,3,800,1200)图片输入到resnet50中进行特征提取,输出shape=(b,1024,25,38)
- 通过1x1卷积降维,变成(b,256,25,38)
- 利用sincos函数计算位置编码
- 将图像特征和位置编码向量相加,作为编码器输入,输出编码后的向量,shape不变
- 初始化全0的(100,b,256)的输出嵌入向量,结合位置编码向量和query_embed,进行解码输出,解码器输出shape为(6,b,100,256),后面的解码器接受该输出,然后再次结合置编码向量和query_embed进行输出,不断前向
- 将最后一个解码器输出输入到分类和回归head中,得到100个无序集合
- 对100个无序集合进行后处理,主要是提取前景类别和对应的bbox坐标,乘上(800,1200)即可得到最终坐标
3.3 Swin Transformer
Transformer 从 NLP 迁移到 CV 上没有大放异彩主要有两点原因:
- 最主要的原因是两个领域涉及的scale不同,NLP 任务以 token 为单位,scale 是标准固定的,而 CV 中基本元素的 scale 变化范围非常大。
- CV 比起 NLP 需要更大的分辨率,而且 CV 中使用 Transformer 的计算复杂度是图像尺度的平方,这会导致计算量过于庞大, 例如语义分割,需要像素级的密集预测,这对于高分辨率图像上的Transformer来说是难以处理的。
Swin Transformer 就是为了解决这两个问题所提出的一种通用的视觉架构。Swin Transformer 引入 CNN 中常用的层次化构建方式。
图片预处理:分块和降维 (Patch Partition)
Swin Transformer 首先把𝑯∗𝑾∗𝑪的图片,变成一个𝑵∗( $ \begin{equation} 𝒑^𝟐 \end{equation} $ ∗𝑪)的2维的image patches。它可以看做是一系列的展平的2D块的序列,这个序列中一共有𝑯∗𝑾/ $ \begin{equation} 𝒑^𝟐 \end{equation} $ 个展平的2D块,每个块的维度是$ \begin{equation}𝒑^𝟐 \end{equation} $ ∗𝑪。其中 𝒑是块大小。
在 Swin Transformer 中,块的大小𝒑=𝟒,所以得到的块的大小𝑵∗𝟒𝟖 ,这里的𝑵= $ \begin{equation} \frac{𝑯∗𝑾}{𝟏𝟔} \end{equation} $ = $ \begin{equation} \frac {𝑯}{𝟒} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟒} \end{equation} $。
所以经过了这一步的分块操作,一张 𝑯∗𝑾∗𝟑的图片就变成了 $ \begin{equation} 𝑯 \over 𝟒 \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟒} \end{equation} $ ∗ 𝟒𝟖的张量,可以理解成是 $ \begin{equation} \frac {𝑯}{𝟒} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟒} \end{equation} $个图片块,每个块是一个 𝟒𝟖 维的 token。
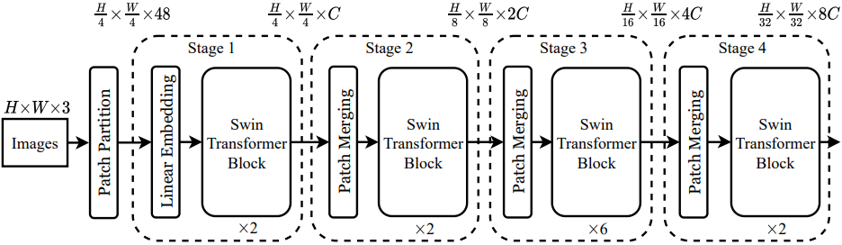
Stage 1:线性变换 (Linear Embedding)
现在得到的向量维度是:$ \begin{equation} \frac {𝑯}{𝟒} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟒} \end{equation} $ ∗ 𝟒𝟖 ,还需要做一步叫做Linear Embedding的步骤,对每个向量都做一个线性变换(即全连接层),变换后的维度为 𝑪 。这一步之后得到的张量维度是:$ \begin{equation} \frac {𝑯}{𝟒} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟒} \end{equation} $ ∗ 𝑪
Stage 1:Swin Transformer Block
接下来 $ \begin{equation} \frac {𝑯}{𝟒} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟒} \end{equation} $ ∗ 𝑪 这个张量进入2个连续的 Swin Transformer Block 中,这被称作 Stage 1,在整个的 Stage 1 里面 token 的数量一直维持 $ \begin{equation} \frac {𝑯}{𝟒} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟒} \end{equation} $ 不变
一个 Swin Transformer Block 由一个带两层 MLP 的 Window-based MSA 组成,另一个 Swin Transformer Block 由一个带两层 MLP 的 Shifted Window-based MSA 组成
Stage 1:Swin Transformer Block:Window-based MSA
标准 ViT 的多头注意力机制 MSA 采用的是全局自注意力机制,即:计算每个 token 和所有其他 token 的 attention map。全局自注意力机制的计算复杂度是 O(𝑵^𝟐∗𝒅) ,其中, 𝑵是 token的数量, 𝒅是 Embedding dimension。全局自注意力机制的计算复杂度与序列长度𝑵成平方关系。当图片分辨率较高或是密集预测任务中计算量会过大。
Window-based MSA 不同于普通的 MSA,它在一个个 window 里面去计算 self-attention。假设每个 window 里面包括𝑴∗𝑴个 image patches,则 Window-based MSA 和普通的 MSA 的计算量分别为:
\begin{equation} 𝛀(𝑴𝑺𝑨)=𝟒𝒉𝒘𝑪^𝟐+𝟐(𝒉𝒘)^𝟐 𝑪 \end{equation}
\begin{equation} 𝛀(𝑾−𝑴𝑺𝑨)=𝟒𝒉𝒘𝑪^𝟐+𝟐𝑴^𝟐 𝒉𝒘𝑪 \end{equation}
由于 Window 的 patch 数量 𝑴远小于图片patch数量 𝒉𝒘,Window-based MSA 的计算量与序列长度 𝐍=𝒉𝒘成线性关系。
Stage 1:Swin Transformer Block:Shifted Window-based MSA
Window-based MSA 虽然大幅节约了计算量,但是牺牲了 windows 之间关系的建模,不重合的 Window 之间缺乏信息交流影响了模型的表征能力。
为了解决这一问题,在两个连续的Swin Transformer Block中交替使用W-MSA 和 SW-MSA。将前一层 Swin Transformer Block 的 8x8 尺寸feature map划分成 2x2 个patch,每个 patch 尺寸为 4x4,然后将下一层 Swin Transformer Block 的 Window 位置进行移动,得到 3x3 个不重合的 patch。移动 window 的划分方式使上一层相邻的不重合 window 之间引入连接,大大的增加了感受野。
在新的 window 里面做 self-attention 操作,就可以包括原有的 windows 的边界,实现 windows 之间关系的建模。
引入 Shifted Window 会带来另一个问题就是会造成 window 数发生改变,而且有的 window 大,有的 window 小
解放方案:cycle shift合并小的 windows
经过了 cycle shift 的方法,一个 window 可能会包括来自不同 window 的内容。比右下角的 window,来自4个不同的 sub-window。因此,要采用 masked MSA 机制将 self-attention 的计算限制在每个子窗口内。最后通过 reverse cycle shift 的方法将每个 window 的 self-attention 结果返回
cycle shift过程:按照之前的 window 划分,就能够得到 window 5 的attention 的结果了。但是这样操作会使得 window 6 和 4 的 attention 混在一起,window 1,3,7 和 9 的 attention 混在一起。所以需要采用 masked MSA 机制将 self-attention 的计算限制在每个子窗口内,如何实现?
按照 Swin Transformer 的代码实现 ,还是做正常的 self-attention (在 window_size 上做),之后要进行一次 mask 操作,把不需要的 attention 值给它置为0
Stage 2/3/4
Stage 2 的输入是维度是 $ \begin{equation} \frac {𝑯}{𝟒} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟒} \end{equation} $ ∗ 𝑪 的张量。从 Stage 2 到 Stage 4 的每个 stage 的初始阶段都会先做一步 Patch Merging 操作,Patch Merging 操作的目的是为了减少 tokens 的数量,它会把相邻的2×2个 tokens 给合并到一起,得到的 token 的维度是 𝟒𝑪 。Patch Merging 操作再通过一次线性变换把维度降为𝟐𝑪 。至此,维度是 $ \begin{equation} \frac {𝑯}{𝟒} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟒} \end{equation} $ ∗ 𝑪 的张量经过Patch Merging 操作变成了维度是 $ \begin{equation} \frac {𝑯}{𝟖} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟖} \end{equation} $ ∗ 𝟐𝑪 的张量。
同理,Stage 3 的Patch Merging 操作会把维度是 $ \begin{equation} \frac {𝑯}{𝟖} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟖} \end{equation} $ ∗ 𝟐𝑪 的张量变成维度是 $ \begin{equation} \frac {𝑯}{𝟏𝟔} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟏𝟔} \end{equation} $ ∗ 𝟒𝑪 的张量。Stage 4 的Patch Merging 操作会把维度是 $ \begin{equation} \frac {𝑯}{𝟏𝟔} \end{equation} $ ∗ $ \begin{equation} \frac {𝑾}{𝟏𝟔} \end{equation} $ ∗ 𝟒𝑪 的张量变成维度是 $ \begin{equation} \frac {𝑯}{𝟑𝟐} ∗ \frac {𝑾}{𝟑𝟐} \end{equation} $ ∗ 𝟖𝑪 的张量。
每个 Stage 都会改变张量的维度,形成一种层次化的表征。因此,这种层次化的表征可以方便地替换为各种视觉任务的骨干网络。
Swin Transformer 的位置编码
Swin Transformer 的位置编码加在 attention 矩阵上
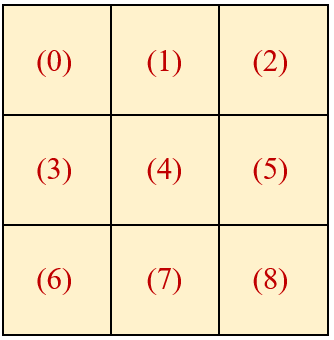
- 位置编码𝑩的第(𝒊,𝒋)个元素𝑩(𝒊,𝒋) ,它代表的是 Window 里面第𝒊个 Patch 和第𝒋个 Patch 的相对位置关系。
- 所以应该有𝑩(𝟑,𝟕)=𝑩(𝟒,𝟖)=𝑩(𝟏,𝟓)=𝑩(𝟎,𝟒),因为它们都代表着斜对角的位置关系。
- 所以应该有 𝑩(𝟎,𝟔)=𝑩(𝟏,𝟕)=𝑩(𝟐,𝟖) ,因为它们都代表着上下有间隔的位置关系。
- ……